Reports Area L
Research Stay in Brest by Mariana Lage (Dec 22)

One of the best parts of being a scientist in my opinion is to go abroad, meet new researchers and discuss ideas. It is amazing to see what other scientists are doing and how different the institutes are. Last year I had the opportunity to go to Ifremer (Institut français de recherche pour l'exploitation de la mer), in Brest, Brittany, France, and all started with a simple email to Claire Ménesguen introducing myself and asking whether I could visit the institute.
Claire is one of the team leaders of the Ocean Scale Interactions group at the Laboratory for Ocean Physics and Satellite remote sensing (LOPS) together with Jonathan Gula. The main focus of the group is to study ocean dynamics with a particular interest in small horizontal and temporal scales. Once the collaboration was settled and I arrived in Brest, we had several meetings to start planning the structure of the upcoming work. The infrastructure at Ifremer is great, and I met many PhD students and posdocs. As the time and work progressed, we decide to slightly modify our initial plan. Science is highly non-linear, so we had to adapt given the results we obtained with some of the analyses. The good part about that is that I was able to constantly discuss not only with Claire (and Jeff), but also with a lot of people from both Ifremer and LOPS. Because people have different backgrounds, we were able to approach my research topic from many different angles, which led to many nice ideas.
Apart from work (because it would be a shame not to enjoy Brittany’s landscape), I enjoyed the weekends hiking and traveling to small cities around Brest, and, of course, eating! Brittany is very well-known for crêpes, sea food (oysters!) and caramel, which are musts to try when you are there. Brest is on the west coast of France and the landscape is just stunning! The color of the water, the lighthouses and the shape of the coast make this city quite unique. There is also an Aquarium which is really worth visiting. One curiosity from there is that they have their own language (Breton, or Brezhoneg), although nowadays French is the main language spoken. Another curiosity is that it rains a lot, and the weather can easily change from heavy storm to shining sun in a matter of hours.
After my return, Claire and I are still in close contact and we are already planning the next steps regarding our collaborative research. My time there was really pleasant and fruitful and a second research stay is planned in October 2023. I really recommend sometime abroad for everyone especially because the TRR provides the most difficult thing to get: money. This is a unique opportunity to gather different opinions about one’s research topic and to get people to know you too. I left behind many open doors and I am really excited to continue working with all the people I met!
Decomposition of Vertical Momentum Fluxes in the Tropical Atmosphere
Based on MODES we will develop a tool for the computation of vertical momentum fluxes from high-resolution ERA5 data.
Greetings dear reader! My name is Valentino and I work as a PhD student at the University of Hamburg under the supervision of Dr. Nedjeljka Žagar (Universität Hamburg). I am a part of the TRR subproject L2 named “Quantifying Dynamical Regimes in the Ocean and the Atmosphere”. I am originally from Croatia where I spent all of my education years. I have Bachelor in Physics/Geophysics from the University of Zagreb and a Masters in Meteorology and Physical Oceanography that I acquired with the thesis on “Implementation of the empirical orthogonal functions analysis to determine nonstationarity of time series” from the University of Zagreb.
I started my work as a part of TRR in May of 2021. with the goal of my work being the quantification of vertical momentum fluxes in the tropical atmosphere. To do this we will employ normal mode decomposition ( NMD ) to decompose atmospheric motions to different dynamical regimes. More precisely we will be using the MODES NMD package developed by Žagar et al., for the horizontal velocity and an associated novel spectral approach for the vertical velocity decomposition. Based on MODES we will develop a tool for the computation of vertical momentum fluxes from high-resolution ERA5 data.
Then, we will analyze climate models in the same way and compare the results with those for reanalysis to quantify missing momentum fluxes across scales. The results will be then used to quantify the missing momentum fluxes in climate models that are still running at a much lower resolution. The quantification of vertical momentum fluxes associated with the inertiagravity waves in analysis data can become valuable validation metrics of new parameterizations and upscale transfers in ICON-a and other climate models. The results will provide, among others, a novel scaledependent quantification of the vertical momentum fluxes associated with different atmospheric regimes in analyses and climate models.
Upper-ocean energy spectrum, flux & dissipation
The use of a new technology combined with new sampling algorithms potentially offers unprecedented insights into deep ocean mixing and internal wave climate.
Hi! My name is Ilmar and I work as a PhD student at the MARUM/University of Bremen. I am supervised by Dr. Maren Walter (MARUM/University of Bremen) and Dr. Alexa Griesel (Universität Hamburg) and am part of the TRR subprojects L3
entitled “Meso- to Submesoscale Turbulence in the Ocean” and W5 „Internal Wave Energy Dissipation and Wavenumber Spectra: Adaptive Sampling in the Ocean Interior “.
Before I joined TRR, I lived in Kiel, where I got a bachelor degree in Physics of Earth and master degree in Climate Physics: Meteorology and Physical Oceanography at Christian Albrechts University Kiel & GEOMAR. I started my work as a part of TRR in September 2022.
In the first phase of L3, we assessed turbulence regimes with a focus on the Benguela upwelling region. Using a new scaling method and with adequate subsampling of the deployed surface drifters, we estimated a consistent energy transfer rate and identified an inverse cascade for scales 30-500 km close to the upwelling current. Now Our aim in the second phase is to extend the Lagrangian analyses and apply the structure-function diagnostic (in addition to the classical Lagrangian dispersion estimates) in an area offshore from the Benguela region that is characterized by high internal tide and eddy activity but without a deep baroclinic current. In a concerted effort (targeted measurements with gliders, ship ADCP, drifters) we will quantify horizontal wavenumber spectra for the upper ocean in the Walvis Ridge Region in close collaboration with W5 and W2. The subsampling methods developed from the analyses in the Benguela and Walvis Ridge regions, together with high-resolution modelling, will be used to extrapolate to the global ocean using the global drifter program.
The W5 Project is concerned with the shape of the internal wave energy spectrum, where our aim is to simultaneously observe the oceanic energy spectrum below the submesoscale range and the spatial distribution of energy dissipation, using adaptive/reactive sampling to guide the observations. For this purpose, we will deploy a new hybrid pelagic glider (developed by Prof. Ralf Bachmayer) using an innovative approach of combining advanced numerical model informed sampling techniques in real-time to observe internal wave spectra and turbulence in the ocean interior. As a key sensor, a pressure rated microstructure probe will be integrated into the pelagic glider system; this use of a new technology combined with new sampling algorithms potentially offers unprecedented insights into deep ocean mixing and internal wave climate. Obtained observational data will be contextualized by idealized and regional numerical modelling studies carried out in L3 and L2 and the results of this project will complement the observations, that will be jointly used to construct the upper- and pelagic oceanic energy spectrum within L3, and the observations towards obtaining a local energy budget.
Investigating eddy diffusivitites and eddy-mean flow interactions
Our observational data will serve the model as a reference that includes smaller scales that the model is not able to cover.
In September 2016 I started working as a postdoctoral researcher in the subproject L3 Diagnosing and parameterising the effects of eddies at the Universität Hamburg with Kerstin Jochumsen from Experimental Oceanography and Alexa Griesel from Theoretical Oceanography. Having a background in nonlinear dynamics and statistical physics in application to complex systems, I am strongly attracted by the aim of our research project and by the possibility to work within an inspiring interdisciplinary research network as created by the TRR181 with its great possibilities for exchange with scientists of different fields.
A major link to my former research consists in the analysis of trajectories (derived from in situ experiments or modeled by stochastic processes) and more specifically the analysis of broad (non Gaussian) Langrangian statistics of absolute and relative dispersion. The goal of our research subproject L3 is the quantification of eddy diffusivities and eddy-mean flow interactions by using Langrangian particles statistics in both eddying ocean models and observations. Its aim is to develop and to test energy consistent parameterisations of meso- and sub-mesoscale processes for the global ocean with a focus on 100 km -1 km scales.
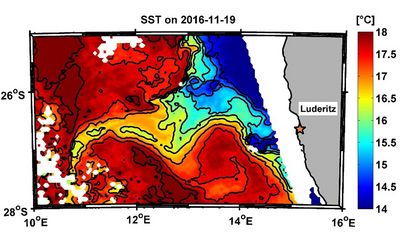
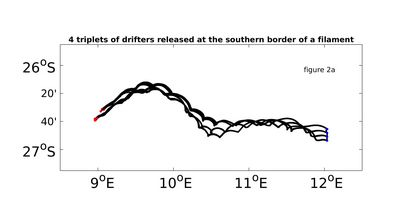
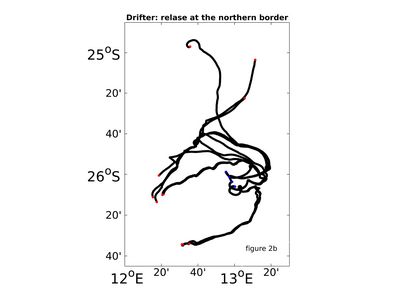
At the beginning I developed and tested float deployment strategies by means of the high resolution POP model. In November/December 2016 our cruise with the RV Meteor took place in the atlantic-sea off the african coast. The cold upwelling front off Namibia's coast in the area of Luderitz has a highly irregular structure due to eddies and filaments, finger-like structures of cold upwelling water pushing west into the warm surface waters offshore (see Figure 1). In our field experiment we explored mesoscale and submesoscale structures within a filament by satellite-tracking 37 surface drifters which we released in groups of triplets. As a first result we find that, due to the underlying rich mesoscale system, the dispersion statistics are very different depending on the location of release. While the drifters of the group released at the southern border of the filament separate slower (Figure 2a), the drifters in the group released closer to the upwelling system at the northern border of the filament separate faster from each other and follow distinct paths within the complex surface currents (Figure 2b). Currently our research focuses on the relative dispersion of drifter pairs (and its corresponding probability density function) as its properties depend on the kinetic energy spectrum. The statistical analyzing of single particle dispersion and the comparison of our findings with dispersion statistics of ocean model will be a next step. Here our observational data will serve the model as a reference that includes smaller scales that the model is not able to cover.
More Information about the research cruise on RV Meteor (M132) including reports, posters and videos of the scientific work have a look have a look at our TRR181 homepage.
Research Stay in Perth by Mira Schmitt (Oct 23)

At the end of last year, I spent two months in Perth, Western Australia, to work on a collaborative project with Jen-Ping Peng, who was a PhD in TRR181’s first phase and is now a PostDoc in the working group of Nicole Jones at the Indian Ocean Marine Research Centre of the University of Western Australia. For the most part, my stay in Perth was covered by the Australia–Germany Joint Research Cooperation Scheme, with the TRR kindly providing some additional financial support. The above scheme is an initiative of Universities Australia and the German Academic Exchange Service (DAAD) for the support of international academic cooperation. Early-career researchers from Australia and Germany are encouraged to hand in proposals for a joint research topic, and, if approved, the grant covers the expenses for a research stay at the partner institute. For our project, Jen-Ping and I decided that we want to combine our two fields of research and investigate the interactions of diurnal warm layers, submesoscale fronts and other turbulent processes in the surface mixed layer. For this, we firstly extended the 1D turbulence model GOTM to include 3D frontal effects and validated our model results by comparing them to published LES studies. Then, we used our model to recreate measurements taken previously during two campaigns in the Baltic Sea and the Indian Ocean and use the results to understand the governing processes involved. We found nice agreements between the measurements and our simple model and are planning on publishing two joint papers on these topics.
But besides the work aspect, Western Australia was also a great place to explore and spend time. Jen-Ping was an excellent host (I think we went to every great Asian restaurant in all of Perth) and the weather was pleasant from beginning to end (basically nothing but sunshine for two months). I stayed in a researcher accommodation on campus, which is located a few kilometres away from the city centre directly at the Swan river estuary with lots of green areas and beautiful old trees. Moreover, I got to go on two nice road trips up and down the coast, explore the Margaret River wine region, see quokkas on Rottnest Island and snorkel in the beautiful Ningaloo Reeve national reserve with an infinite amount of fish, stingrays and even a big sea turtle. I also got to see a living colony of stromatolites, microorganisms that are believed to be the oldest form of life on earth dating back 3 billion years, and that can only survive in hypersaline estuaries like Shark Bay in Western Australia. And while there were a few snake and spider sightings, I didn’t have the heart to look up their level of toxicity, so I like to believe it was all safe and sound.
I can definitely recommend looking into the Joint Research Cooperation Scheme (it exists not only between Germany and Australia, but also other countries) and would strongly encourage others to take the opportunity to extend their network and travel, maybe to Perth, it’s a lovely corner of the world. I would like to thank Jen-Ping, Nicole Jones and all other members of this working group for hosting me, showing interest in my research and teaching me about their fields of research.
Diurnal Warm Layers and Rain Layers: Dynamics, Turbulence and Atmospheric Feedbacks
My work so far has been to simulate idealized cases using a 1D turbulence model.
Hello everyone, my name is Mira, I am a PhD at the Institute for Baltic Sea Research in Warnemünde and working in subproject L4, supervized by Lars Umlauf. To start off with something about myself: I studied physics at the University of Göttingen with a focus on Astro- and Geophysics during my masters. After an internship on sea ice physics at the University of Otago in New Zealand, I studied double-diffusive convection during my master thesis.
I love hiking and backpacking, so before, during and after my studies I spent a lot of time abroad, travelling, discovering new countries and meeting interesting people. When the pandemic started I had to change my plans and, by a chain of coincidences, started this phd position, which I am very happy about. I very much enjoy to live this close to the ocean and I spend a lot of time by the beach.
The focus of my project is on diurnal warm layers and rain layers on the ocean surface. These thin, stratified layers influence air-sea fluxes and turbulence in the ocean interior, but are usually not resolved in climate models. My work so far has been to simulate idealized cases using a 1D turbulence model. With that I can identify the non-dimensional parameters that govern these processes and perform parameter space studies, which can be the basis for a parameterization. I also work in close collaboration with Mira Shevchenko and Cathy Hohenegger, who study diurnal warm layers and their effect on the atmosphere using the coupled ICON model.



