M1: Dynamical Systems Methods and Reduced Models in Geophysical Fluid Dynamics
Principal investigators: Prof. Ingenuin Gasser (Universität Hamburg), Prof. Jens Rademacher (Universität Hamburg)
Objectives
We study the multi-scale nature of geophysical flows from a mathematical perspective
Energy is distributed across a wide range of scales which are not all properly resolved and whose interactions are only partially understood.
- We use asymptotic methods for clarifying the emergence of different regimes of motion and their corresponding instabilities to greatly improve our understanding of the link between the micro-mesoscopic and macroscopic properties of turbulent geophysical flows.
- Central in our analyses are so-called covariant Lyapunov vectors (CLVs) which are objects that describe instabilities and statistical mechanics based on rigorous mathematical theory.
- We foster the mathematical foundation of CLV algorithms to validate numerical results, to improve existing algorithms, and to develop new algorithms that help to describe scale-interactions.
Climate models cannot resolve the smallest scales due to a lack of computational power. To incorporate the missing scales some of the TRR181’s target operational models for large scales entail small-scale ‘subgrid’ models and parametrizations.
- We address the mathematical foundation and properties of parameterized PDEs (PPDEs) to provide a more fundamental understanding of the TRR181’s target operational models and to gain new insight into their crucial dynamical features.
- Based on a unified framework of PPDE models, we pave the way towards implementing CLV methods into more comprehensive climate models used in the TRR181.
Phase 1
We improved the mathematical foundations of CLV algorithms
CLVs are the right tool to study instabilities in turbulent regimes. They are natural modes belonging to Lyapunov exponents and encode past and future dynamics along a given background flow. A cornerstone of theoretical studies is the Multiplicative Ergodic Theorem (MET) [1], which provides existence and uniqueness of CLVs. The MET generalizes the classical stability theory for steady states and periodic orbits to more general trajectories.
| classical theory | MET | |
growth rates | eigenvalues / Floquet exponents | Lyapunov exponents |
| directions | eigenvectors / Floquet vectors | CLVs |
| spaces | eigenspaces / Floquet spaces | Oseledets spaces |
Convergence proof of Ginelli’s algorithm
We derived the first mathematically rigorous convergence proof of the most used CLV algorithm: Ginelli’s algorithm [2]. Our convergence proof relates the speed of convergence to the Lyapunov exponents. We proved that Ginelli’s algorithm approximates CLVs exponentially fast with a rate given by the spectral gap between associated Lyapunov exponents. While the convergence theorem is formulated for Ginelli’s algorithm, we constructed general tools that can be applied to analyze other CLV algorithms as well.
→ more details in our article “A projector-based convergence proof of the Ginelli algorithm for covariant Lyapunov vectors” [3]
From discrete to continuous time
In addition to the pure convergence statement, we also investigated how the algorithm behaves in the transition from discrete to continuous time. It turns out that the algorithm converges for almost every initial configuration in discrete-time settings, while the convergence in continuous-time settings is only in measure. A slight difference that can help to interpret unexpected outputs of the algorithm.
→ more details in our article “A projector-based convergence proof of the Ginelli algorithm for covariant Lyapunov vectors” [3]
From finite to infinite dimensions
Another important aspect in the analysis of CLV algorithms is the transition from finite to infinite dimensions of the underlying dynamical system. Many applications in geosciences require increased amounts of system variables through, e.g., finer grid sizes or higher spectral modes. This results in a higher dimension and affects CLVs and their computation. While there is still a large gap in understanding CLV algorithms in the transition from finite to infinite dimensions, we succeeded in taking first steps by proving a convergence statement for Ginelli’s algorithm on Hilbert spaces. Our result builds upon so-called semi-invertible METs, which allow for non-invertible linear propagators and among others are used in the context of Perron-Frobenius operators to describe mixing in the ocean [4, 5].
→ more details in our article “Computing covariant Lyapunov vectors in Hilbert spaces” [6]
References:
[1] Oseledets, V. I. (1968). A multiplicative ergodic theorem. Characteristic Ljapunov, exponents of dynamical systems. Transactions of the Moscow Mathematical Society, 19, 197–231.
[2] Ginelli, F., et.al. (2007). Characterizing Dynamics with Covariant Lyapunov Vectors. Physical review letters, 99, 130601, doi.org/10.1103/PhysRevLett.99.130601.
[3] Noethen, F. (2019). A projector-based convergence proof of the Ginelli algorithm for covariant Lyapunov vectors. Physica D, 396, 18–34, doi.org/10.1016/j.physd.2019.02.012.
[4] González-Tokman, C. & Quas, A. (2014). A semi-invertible operator Oseledets theorem. Ergodic Theory and Dynamical Systems, 34(4), 1230–1272, doi.org/10.1017/etds.2012.189.
[5] González-Tokman, C. (2018). Multiplicative ergodic theorems for transfer operators: Towards the identification and analysis of coherent structures in non-autonomous dynamical systems. In: Contributions of Mexican mathematicians abroad in pure and applied mathematics. Ed. by Galaz-García, F., Millán, J. C. P. & Solórzano, P. Contemporary Mathematics, 709, 31–52, doi.org/10.1090/conm/709/14290.
[6] Noethen, F. (2019). Computing covariant Lyapunov vectors in Hilbert spaces. arXiv: 1907.12458.
We analyze the coupled ocean-atmosphere dynamics based on CLVs
While Lyapunov exponents describe how fast linear perturbation grow or decay in a chaotic system, the Covariant Lyapunov Vectors (CLVs) point into the directions of these perturbations. Thus, CLVs are physically relevant; they reveal the local geometrical structure of the system’s attractor and the basic properties of the dynamics at the same time. In our previous research, we have reinterpreted the Lorenz energy cycle in a quasi-geostrophic atmospheric model based on CLVs [1], and we have analyzed the CLVs in case of blocking events [2].
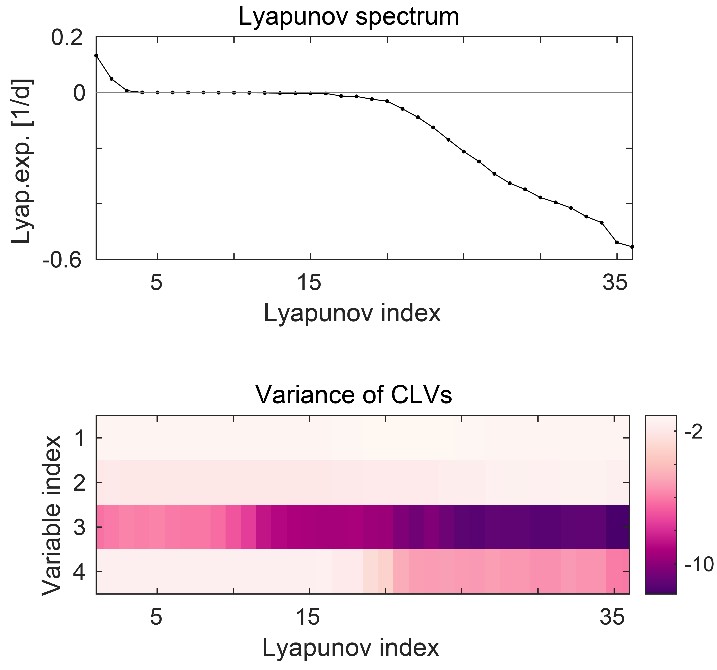
We analyze the dynamics of the quasi-geostrophic coupled ocean-atmosphere model MAOOAM [3], and calculate the CLVs based on Ginelli’s algorithm [4]. The spectrum of Lyapunov exponents reveals the existence of an extended center subspace with several near-zero Lyapunov exponents, corresponding to the slow dynamics of the system (Figure 1). This is similar to what was found in [5], however, in our study, we go deeper in the analysis of the system dynamics based on CLVs, and we consider higher model resolutions too. In a low-order version (10 atmospheric and 8 oceanic modes), MAOOAM exhibits a regime behavior. The system oscillates between a chaotic and a very weakly chaotic (almost quasi-periodic) state. Based on the CLVs, we can understand these alternating dynamics. We find that, while in the chaotic regime the atmospheric model variables are dominant in the development of instabilities, in the weakly chaotic regime the ocean thermodynamic variables prevail.
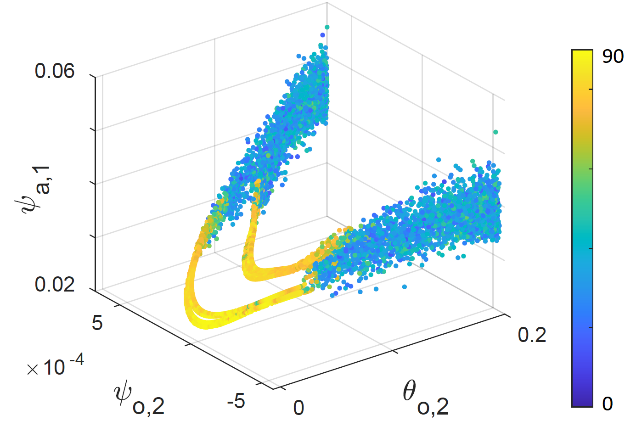
Angles between CLVs and between subspaces spanned by CLVs provide useful information about the system dynamics as well. It is interesting that, when our system enters the weakly chaotic regime, the first CLV seems to align with the CLVs of the center subspace, i.e. it shows in the direction of the flow. Similar behavior was found in very low-dimensional systems before critical transitions [6]. We also find that the angle between subspaces spanned by CLVs changes with the regime. Based on the angle between subspaces split at an appropriate CLV we can separate the two dynamical regimes (Figure 1). The Lyapunov spectrum changes from 3 positive Lyapunov exponents and 17 near-zero exponents, in case of the chaotic regime, to 1 positive (very small, almost undistinguishable from 0) Lyapunov exponent and 15 near-zero exponents for the weakly chaotic regime, in which the contribution of the ocean thermodynamic variable predominates the development of instabilities. The rest of the Lyapunov exponents are negative in both regimes.
In a higher spectral resolution of MAOOAM (55 atmospheric and 25 oceanic modes), we find also a close relationship between the dynamics of the system and the angles between CLVs and subspaces. However, this relationship seems to be very different compared to the low-order version, and needs further investigations.
References:
[1] Schubert, S. and Lucarini, V. (2015): Covariant Lyapunov vectors of a quasi-geostrophic baroclinic model: Analysis of instabilities and feedbacks, Q. J. Roy. Meteor. Soc., 141, 3040–3055, https://doi.org/10.1002/qj.2588.
[2] Schubert, S. and Lucarini, V. (2016): Dynamical analysis of blocking events: spatial and temporal fluctuations of covariant Lyapunov vectors, Q. J. Roy. Meteor. Soc., 142, 2143–2158, https://doi.org/10.1002/qj.2808.
[3] De Cruz, L., Demaeyer, J., and Vannitsem, S. (2016). The Modular Arbitrary-Order Ocean-Atmosphere Model: MAOOAM v1.0, Geosci. Model Dev., 9, 2793–2808,
https://doi.org/10.5194/gmd-9-2793-2016.
[4] Ginelli, F., et.al. (2007). Characterizing Dynamics with Covariant Lyapunov Vectors. Physical review letters, 99, 130601, doi.org/10.1103/PhysRevLett.99.130601.
[5] Vannitsem, S. and Lucarini, V. (2016). Statistical and Dynamical Properties of Covariant Lyapunov Vectors in a Coupled Atmosphere– Ocean Model – Multiscale Effects, Geometric Degeneracy, and Error Dynamics, J. Phys. A-Math. Theor., 49, 224001, https://doi.org/10.1088/1751-8113/49/22/224001.
[6] Sharafi, N., Timme, M and Hallerbeg, S. (2017). Critical transitions and perturbation growth directions, Physical Review E, 96, 032220, https://doi.org/10.1103/PhysRevE.96.032220.
Reports
Research Stay in Texas by Paul Holst (April 23)

In April this year, I had the unique opportunity to enjoy a 2-week stay in College Station, USA, at Texas A&M University to visit Edriss Titi, who is a professor of nonlinear mathematical science. Professor Edriss Titi is a worldwide renowned applied mathematician who specializes in the mathematical study of problems from fluid dynamics, nonlinear partial differential equations, and in a dynamical systems approach to turbulence. His contributions to these areas are of the highest calibre and practical impact.
After hearing about Edriss Titi's expertise a few months before my research stay and after a simple email to him in which I briefly introduced myself and my research work, a good exchange of information with him developed, I was already very excited to do research together with him and learn from him during the research stay planned shortly thereafter in April. When I arrived in Texas shortly after Easter in April, we started working together on my research topic almost immediately. We talked daily at selected times from then on and made good progress. I greatly benefited from the conversations with him and learned new methods and aspects of my research topic and, even more generally, of the topics in my research area. The conversations I had with Xin Liu, one of the postdocs in Edriss Titi's research group at Texas A&M University, were also very helpful. At the end of my time in Texas, our conversations even resulted in a meaningful outcome regarding my research topic.
In between the meetings I had with Edriss Titi, I worked a lot on the exercises he gave me as well as a lot on my research topic. Away from my research work, I mostly explored the town of College Station on a bicycle in my scarce free time. During these explorations, I especially remembered a couple of beautiful green parks that College Station has to offer, as well as the impressive mansion district. There were also long distances that I had to travel to get from one place to another in College Station. This then gave me a sense, in those moments when I was out of breath, of why even many local people thought you needed a car to get from A to B in Texas.
After my return, I was very happy with the experience, knowledge, and results I was able to gain in Texas. The whole experience I had there has advanced me both scientifically and personally. I am very grateful for this and can therefore only recommend that everyone take advantage of the opportunity of a research stay.
Screening The Coupled Atmosphere-Ocean System Based On Covariant Lyapunov Vectors
I use the tangent linear version of the coupled atmosphere-ocean quasi-geostrophic model MAOOAM, and calculate the CLVs based on the so-called Ginelli method.
Covariant Lyapunov vectors (CLVs) reveal the local geometrical structure of the systems‘s attractor, thus providing valuable information about the basic dynamics. They are physically meaningful since they point into the directions of linear perturbations applied to the trajectory of the system. CLVs are linked to Lyapunov exponents, which describe the growth or decay rate of linear perturbations.
My name is Melinda Galfi, and I am a postdoc in the M1 subproject. I am continuing the work on CLV analysis started by Sebastian Schubert. I use the tangent linear version of the coupled atmosphere-ocean quasi-geostrophic model MAOOAM, and calculate the CLVs based on the so-called Ginelli method. I compute the CLVs in the phase space of the model, spanned by the spectral model variables, which can be grouped into four different categories: atmospheric dynamic and thermodynamic variables, as well as oceanic dynamic and thermodynamic variables.
The spectrum of Lyapunov exponents of our systems reveals the existence of a central or slow manifold. This is a basic property of coupled ocean-atmosphere models, and has to do with the multiscale character of this type of chaotic system. Based on the CLVs, we hope to understand more deeply the dynamical properties of the system itself, and especially of the slow manifold. To achieve this, one can use several CLV based indicators. One of these indicators is the variance of CLVs, showing the contribution of each model variable to the growth or decay of perturbations. By computing the variance of the CLVs in MAOOAM, we see that the atmospheric variables have the strongest contribution to the evolution of perturbations in our system. However, we detect an exception in case of instabilities growing or decaying on long time scales, where the contribution of the oceanic thermodynamic variables is approximately as strong as the one of the atmosphere. This shows that the d y n a m i c s of the slow manifold is governed by interactions between atmosphere and ocean, with the main coupling taking place through the ocean thermodynamics. The contribution of the ocean is the strongest in case of perturbations decaying over long time scales. Another useful indicator is the angle between CLVs, revealing the local structure of the attractor. Our results show that the angle between the CLVs corresponding to the slow manifold is dominantly very near zero, hinting to multiscale instabilities and geometrical degeneracies.
As a next step, we would like to repeat the CLV analysis for a substantially higher model resolution. The currently used resolution consists of 5x5 atmospheric and 5x5 oceanic modes. Our final goal is to study the energy transfers between atmosphere and ocean based on CLVs.
Publications
Holst, P., Rademacher, J.D.M. & Yang, J. (2024). Rotating convection with horizontal kinetic energy backscatter, accepted.
Noethen, F. (2022). Well-Separating Common Complements for Sequences of Subspaces of the Same Codimension are Generic in Hilbert Spaces. Anal. Math., doi: https://doi.org/10.1007/s10476-022-0124-z.
Noethen, F. (2021). Computing Covariant Lyapunov Vectors in Hilbert spaces. J. Comput. Dyn., 2021, 8 (3): 325-352. doi: 10.3934/jcd.2021014.
Lucarini, V. (2019). Stochastic Resonance for Non-Equilibrium Systems, J. Adv. Model. Earth Sys. doi: https://doi.org/10.1029/2019MS001855.
Lucarini, V. and Gritsun, A. (2019). A New Mathematical Framework for Atmospheric Blocking Events, Clim. Dynam., 1-24, doi:10.1007/s00382-019-05018-2.
Noethen, F. (2019). Computing covariant Lyapunov vectors in Hilbert spaces. arXiv: 1907.12458.
Noethen, F. (2019). Well-separating common complements of a sequence of subspaces of the same codimension in a Hilbert space are generic, arXiv:1906.08514
Carlu, M., Ginelli, F., Lucarini, V., & Politi, A. (2019). Lyapunov analysis of multiscale dynamics: the slow bundle of the two-scale Lorenz 96 model. Nonlinear Proc. Geoph., 26, 73-89, https://doi.org/10.5194/npg-26-73-2019 .
Lucarini, V., & Bódai, T. (2019). Transitions across Melancholia States in a Climate Model: Reconciling the Deterministic and Stochastic Points of View. Phys. Rev. Lett., 122(15), 158701, doi.org/10.1103/PhysRevLett.122.158701.
Gálfi, V. M., Lucarini, V., & Wouters, J. (2019). A large deviation theory-based analysis of heat waves and cold spells in a simplified model of the general circulation of the atmosphere. J. Stat. Mech.-Theory. E., 2019(3), 033404, https://doi.org/10.1088/1742-5468/ab02e8 .
Noethen, F. (2019). A projector-based convergence proof of the Ginelli algorithm for covariant Lyapunov vectors. Physica D, Vol. 396, p. 18-34, doi: https://doi.org/10.1016/j.physd.2019.02.012.
Biferale, L., Cencini, M., De Pietro, M., Gallavotti, G., & Lucarini, V. (2018). Equivalence of nonequilibrium ensembles in turbulence models. Phys. Rev. E, 98(1), 012202, doi.org/10.1103/PhysRevE.98.012202.
Vissio, G. and Lucarini, V. (2018). Evaluating a stochastic parametrization for a fast--slow system using the Wasserstein distance. Nonlinear Proc. Geoph., 25(2), 413-427, doi.org/10.5194/npg-25-413-2018.
De Cruz, L., Schubert, S., Demaeyer, J., Lucarini, V. & Vannitsem, S. (2018). Exploring the Lyapunov instability properties of high-dimensional atmospheric and climate models, Nonlin. Proc. Geo., 25, 387-412, doi.org/10.5194/npg-25-387-2018.
Vissio, G. & Lucarini, V. (2017). A proof of concept for scale‐adaptive parametrizations: the case of the Lorenz'96 model. Q. J. Roy. Meteor. Soc., 144(710), 63-75, doi.org/10.1002/qj.3184.
Gálfi, V. M., Bódai, T. & Lucarini, V. (2017). Convergence of extreme value statistics in a two-layer quasi-geostrophic atmospheric model. Complexity, 2017, doi.org/10.1155/2017/5340858.
